Інформатика і двійкові коди обчислення. Подання чисельної інформації в ЕОМ. Системи числення. Двійкова система числення

У двійковій системі числення використовуються лише дві цифри 0 і 1. Іншими словами, двійка є підставою двійкової системи числення. (Аналогічно у десятковоїсистеми підставу 10.)

Щоб навчитися розуміти числа в двійковій системі числення, спочатку розглянемо, як формуються числа в звичній для нас десятковій системі числення.

У десятковій системі числення ми маємо в своєму розпорядженні десятьма знаками-цифрами (від 0 до 9). Коли рахунок досягає 9, то вводиться новий розряд (десятки), а одиниці обнуляються і рахунок починається знову. Після 19 розряд десятків збільшується на 1, а одиниці знову обнуляються. І так далі. Коли десятки доходять до 9, то потім з'являється третій розряд - сотні.

Двійкова система числення аналогічна десяткової за винятком того, що в формуванні числа беруть участь всього лише дві знака-цифри: 0 і 1. Як тільки розряд досягає своєї межі (тобто одиниці), з'являється новий розряд, а старий обнуляється.

Переклад чисел з двійкової системи числення в десяткову

Не важко помітити, що в двійковій системі числення довжини чисел зі збільшенням значення ростуть швидкими темпами. Як визначити, що означає ось це: 10001001? Незвичний до такої форми запису чисел людський мозок зазвичай не може зрозуміти скільки це. Непогано б вміти переводити двійкові числа в десяткові.

У десятковій системі числення будь-яке число можна представити у формі суми одиниць, десяток, сотень і т.д. наприклад:

1476 = 1000 + 400 + 70 + 6

1476 = 1 * 103 + 4 * 102 + 7 * 101 + 6 * 100

Подивіться на цю запис уважно. Тут цифри 1, 4, 7 і 6 - це набір цифр з яких складається число 1476. Всі ці цифри по черзі множаться на десять зведену в ту чи іншу ступінь. Десять - це підстава десяткової системи числення. Ступінь, до якої зводиться десятка - це розряд цифри за мінусом одиниці.

Обчислення значення в двійковому поданні

Однією з основних завдань є перетворення десяткових даних в двійкову форму. Для досягнення цієї мети існує кілька методів, і зокрема вони вважаються особливо ефективними в поступовому поділі. Поступово ми ділимо залишок від вихідного цілого числа на два і пам'ятаємо залишки.

Наступний спосіб перетворення числа спочатку ділить вхідну інформацію на десяткові числа і перетворює їх в двійкову форму, використовуючи описану вище процедуру. Таким чином, число 100 перетвориться в три частини - 1, 0 і 0. Кожна третя використовує чотири позиції для зберігання інформації, результатом якої є комбінація.

Аналогічно можна розкласти і будь-двійковечисло. Тільки заснування тут буде 2:

10001001 = 1*27 + 0*26 + 0*25 + 0*24 + 1*23 + 0*22 + 0*21 + 1*20

1*27 + 0*26 + 0*25 + 0*24 + 1*23 + 0*22 + 0*21 + 1*20 = 128 + 0 + 0 + 0 + 8 + 0 + 0 + 1 = 137

Тобто число 10001001 за основою 2 дорівнює числу 137 за основою 10. Записати це можна так:

100010012 = 13710
Чому двійкова система числення так поширена?

Гра вимагає, щоб ми зберігали навіть негативні записи. З простим рішенням приходить принцип вставки спеціального біта, який вказує на наявність знака. Спочатку ми конвертуємо в двійкову форму, а потім додамо відповідний біт в початок. Маючи дійсно цікаве рішення, наступний принцип вимагає знання певної константи. Це додається двійковим після отримання двійковій форми проміжного результату.

Мова як спосіб представлення та передачі інформації

У разі негативних даних для швидкого розрахунку ми використовуємо іншу процедуру. Спочатку ми віднімаємо абсолютне значення вхідних даних з константи в десятковій системі і перетворимо результат в двійкове подання. У разі позитивного числа зворотний код не буде відображений, так як він покладається на стандартне перетворення в двійкову систему. Для негативних даних логічно заперечує всі цифри і додає біт символу 1 в початок.

Справа в тому, що двійкова система числення - це мова обчислювальної техніки. Кожна цифра повинна бути якось представлена ​​на фізичному носії. Якщо це десяткова система, то доведеться створити такий пристрій, який може бути в десяти станах. Це складно. Простіше виготовити фізичний елемент, який може бути лише в двох станах (наприклад, є струм чи ні струму). Це одна з основних причин, чому двійковій системі числення приділяється стільки уваги.
Переклад десяткового числа в двійкове

Переклад чисел з однієї системи числення в іншу

Той же метод має той же принцип, що і зворотний код. Позитивні числа знову залишаються недоторканими. У негативному, це також заперечує цифри і додатково додає двоичное додаткове значення.

Мова як спосіб представлення та передачі інформації

У разі негативних даних для швидкого розрахунку ми використовуємо іншу процедуру. Спочатку ми віднімаємо абсолютне значення вхідних даних з константи в десятковій системі і перетворимо результат в двійкове подання. У разі позитивного числа зворотний код не буде відображений, так як він покладається на стандартне перетворення в двійкову систему. Для негативних даних логічно заперечує всі цифри і додає біт символу 1 в початок.

Може знадобитися перевести десяткове число в двійкове. Один із способів - це поділ на два і формування двійкового числа із залишків. Наприклад, потрібно отримати з числа 77 його двійкову запис:

77/2 = 38 (1 залишок)
  38/2 = 19 (0 залишок)
19/2 = 9 (1 залишок)
  9/2 = 4 (1 залишок)
  4/2 = 2 (0 залишок)
  2/2 = 1 (0 залишок)
  1/2 = 0 (1 залишок)

Збираємо залишки разом, починаючи з кінця: 1001101. Це і є число 77 в двійковому поданні. перевіримо:

1001101 = 1*26 + 0*25 + 0*24 + 1*23 + 1*22 + 0*21 + 1*20 = 64 + 0 + 0 + 8 + 4 + 0 + 1 = 77

1.1 Непозиційної системи числення

1.2 Позиційні системи числення

2. Переклад чисел з однієї системи числення в іншу

2.1 Переклад цілих чисел з однієї позиційної системи числення в іншу

2.2. Переклад правильних дробів

2.3 Переклад неправильних дробів

2.4 Переклад чисел із системи числення в систему з кратним підставою

3. Вибір системи числення для застосування в ЕОМ

4. Двоичная система числення

4.1 Навички поводження з двійковими числами

5. Форми подання двійкових чисел у ЕОМ

6. Точність представлення чисел в ЕОМ

література

Вступ

Тема реферату з курсу «Прикладна теорія цифрових автоматів» - «Представлення чисельної інформації в ЕОМ. Системи числення ».

Мета написання реферату:

ознайомиться з поняттям системи числення; класифікацією систем числення; перекладом чисел з однієї системи числення в іншу; вибором системи числення для застосування в ЕОМ; двійковій системою числення; формами подання двійкових чисел у ЕОМ; точністю представлення чисел в ЕОМ і ін.

1.Поняття системи числення. Класифікація систем числення. Позиційні і непозиційної системи числення

Системи числення були створені в процесі господарської діяльності людини, коли у нього з'явилася потреба в рахунку, а в міру розвитку наукової і технічної діяльності виникла також необхідність записувати числа і щоб між ними чинити обчислення

Системою числення називається сукупність символів і прийомів, що дозволяють однозначно зображати чісла.Ілі, в загальному випадку, це спеціальна мова, алфавітом якого є символи, звані цифрами, а синтаксисом - правила, що дозволяють однозначно сформувати запис чисел. Запис числа в деякій системі числення називається кодом числа. У загальному випадку число записується в такий спосіб:

А = а n a n -1 ... а 2 a 1 а 0

Окрему позицію в записі числа прийнято називати розрядом, а номер позиції - номером розряду, кількість розрядів у записі числа - це розрядність і вона збігається з довжиною числа. З технічної точки зору довжина числа інтерпретується як довжина розрядної сітки. Якщо алфавіт має р   різних значень, то розряд a и в числі розглядається як р-кова цифра, якої може бути присвоєно кожне з р   значень.

Кожній цифрі a и даного числа А однозначно відповідає її кількісний (числовий) еквівалент - К (a і). При будь-якій кінцевій розрядної Секе кількісний еквівалент числа А буде приймати в залежності від клічественних окремих розрядів значення від К (А)   min   до К (А)   max .

Діапазон уявлення (D) чисел в даній системі числення - це інтервал числової осі, укладений між максимальними та мінімальними числами, представленими заданої розрядністю (довжиною розрядної сітки):

D = К (А) (   p )   max - К (А) (   p )   min .

Існує безліч способів запису чисел цифровими знаками. Однак, будь-яка система числення, призначена для практичного використання, повинна забезпечувати:

1) можливість подання будь-якого числа в заданому діапазоні чисел;

2) однозначність подання;

3) стислість і простоту запису чисел;

4) легкість оволодіння системою, а також простоту і зручність оперувати нею.

Залежно від цілей застосування використовують різні системи числення: 2-ю, 10-ю, 8-ю, 16-ю, римську, а для обчислення часу - система числення часу і т.д.

Залежно від способу запису чисел і способу обчислення їх кількісного еквівалента системи числення можна класифікувати наступним чином (рис. 1)

В основному системи числення будуються за наступним принципом:

А (p) = а n р n + а n -1 p n -1 ... .. + а 1 р 1,

де А (p) - запис числа в системі з базисом р і;

а і - база або послідовність цифр системи числення з р i -чним алфавітом

р i - базис системи числення (сукупність ваг окремих розрядів системи числення). Базис десяткової системи числення 10 0, 10 1, 10 2, 10 3, ..., 10 п.

База системи числення може бути позитивною (0,1,2 ... 9), але може бути і змішаної (1,

).

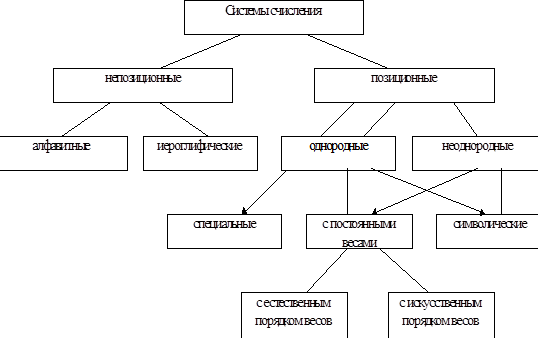
Малюнок. 1 Класифікація систем числення

Підставою системи числення називається кількість різних символів (цифр), що використовуються в кожному з розрядів для зображення числа в даній системі числення.

вага розряду R i  в будь-якій системі числення - це відношення R i = p i / p 0 .

1.1 Непозиційної системи числення

Непозиційної системи числення - це системи числення, алфавіт яких містить необмежену кількість символів (цифр), причому кількісний еквівалент будь-цифри постійний і залежить тільки від появи і не залежить від положення в числі. Такі системи будуються за принципом адитивності, тобто кількісний еквівалент числа визначається як сума цифр в числі. Найбільш відомими представниками непозиційних систем числення є ієрогліфічні і алфавітні, зокрема, ієрогліфічна система - римська система числення. Запис чисел в алфавітних системах числення будується за таким же принципом.

До основних недоліків непозиційних систем числення можна віднести:

1) відсутність нуля;

2) необхідність утримання нескінченної кількості символів;

3) складність арифметичних дій.

Основну увагу приділимо позиційним системам числення.

1.2 Позиційні системи числення

Позиційними називаються такі системи числення, алфавіт яких містить обмежену кількість символів, причому значення кожної цифри визначається не тільки її зображенням, а й перебуває в строгій залежності від позиції в числі. Основна перевага позиційних систем числення - зручність виконання обчислень.

Позиційні системи числення поділяються на ряд підкласів.

Неоднорідні позиційні системи числення (зі змішаним підставою)

У таких системах числення в кожному розряді кількість допустимих символів може бути по-різному значення не залежать один від одного і можуть приймати будь-які значення. Прикладом неоднорідною позиційної системи числення може служити система числення часу, для якої Р 0 - 1 сек, Р 1 - 60 сек, Р 2 - 60 хв, Р 3 - 24 години, Р 4 - 365 діб.

Однорідні позиційні системи числення.

це окремий випадок  позиційних систем числення, в них ваги окремих розрядів представляють собою ряд членів геометричної прогресії зі знаменником p. Тому число в однорідних системах може бути представлено в загальному випадку полиномом виду:

А (p) = а n р n + а n -1 р n -1 + ... а 1 р 1 + а 0 р 0 + а -1 р -1 + ... + а - k р - k,

Підставою однорідної позиційної системи може бути будь-яке ціле число, тому що у визначенні позиційних систем числення не накласти ніяких обмежень на величину підстави. Тому можливо незліченна безліч позиційних систем числення.

Зазвичай число в однорідної системі числення записується в скороченому вигляді:

А (p) = а n а n -1 ... а 1 а 0 а -1 ... а - k,

а назва системи числення визначає її підставу: десятеричная, двійкова, вісімкова, і т.д. Для будь-якої позиційної системи числення справедливо, що її основу зображується символами 10 в своїй системі.

Кодовані системи числення

Це такі системи, в яких цифри однієї системи числення кодуються за допомогою цифр іншої системи. Прикладом може служити двійковій-десяткова система з вагами (8-4-2-1) або (8-4-2-1 + 3).

2. Переклад чисел з однієї системи числення в іншу

Існує два основні методи переведення чисел з однієї системи числення в іншу: табличний і розрахунковий.

Табличний метод прямого перекладу заснований на зіставленні таблиць відповідності чисел різних систем числення. Цей метод дуже громіздкий і вимагає дуже великого об'єму пам'яті для зберігання таблиць, але застосуємо для будь-яких систем числення.

Розрахунковий метод перекладу застосуємо тільки для позиційних однорідних систем числення.

2.1 Переклад цілих чисел з однієї позиційної системи числення в іншу

Нехай задано число А в довільній позиційній системі числення з основою Lі його необхідно перевести в нову систему числення з основою Р, тобто перетворити до вигляду:

А (p) = а n р n + а n -1 р n -1 + ... а 1 р 1 + а 0 р 0, (2.1)

де a i = 0 ÷ (p-1) - база нової системи числення.

Цей вислів можна записати у вигляді:

А = А 1 р + а 0,

де А 1 = (а n р n -1 + а n -1 р n -2 + ... а 2 р 1 + а 1) - ціла частина приватного,

а 0 - залишок від ділення А / р, який є цифрою молодшого розряду шуканого числа.

При розподілі числа А 1 на р отримаємо залишок а 1 і т.д. Іншими словами, якщо записати вираз (2.1) за схемою Горнера:

,

після чого праву частину послідовно розділити на основу нової системи числення р, то отримаємо коефіцієнти:

При цьому розподіл триває до тих пір, поки не виявиться, що

Правило перекладу цілих чисел з однієї позиційної системи числення в іншу формулюється так:

Щоб перевести ціле число з однієї позиційної системи числення в іншу необхідно вихідне число послідовно ділити на основу нової системи числення, записане в вихідної системі числення, до отримання приватного, рівного нулю. Число в новій системі числення записується із залишків від ділення, починаючи з останнього.

Розглянемо як приклад переклад цілого числа 138 в двійкову, вісімкову, шістнадцяткову системи числення.

138, 69, 34, 17, 8, 4, 2, 1, 0 приватна

0 1 0 1 0 0 0 1 - залишок

138, 17, 2, 0- приватне

10 = 2 = 8 = 16

При перекладі з двійкової системи числення в десяткову вихідне число необхідно ділити на основу нової системи, тобто на 1010 2.

Розподіл виконати в двійковій системі важко, тому на практиці зручніше користуватися загальною записом числа у вигляді полінома. При перекладі двійкових чисел в десяткову систему числення зазвичай підраховують суму ступенів підстави 2, при яких коефіцієнти а і рівні 1. Розрахунки при цьому ведуться в десятковій системі.

2.2 Переклад правильних дробів

Нехай правильний дріб А, задану в довільній позиційній системі числення з основою L необхідно перевести в нову систему з основою Р, тобто перетворити її до виду:

А = а -1 р -1 + ... + а - k р - k, (2.2)

якщо, аналогічно перекладу цілих чисел розділити обидві частини виразу на р -1, тобто помножити на р, то отримаємо:

Ар = а -1 + А 1,

де А 1 = а -2 р -1 + а -3 р -2 + ... + а - k р - k +1 - дрібна частина твору,

а -1 - ціла частина результату.

Отримана при цьому цифра цілої частини результату і буде першою цифрою шуканого числа. Помноживши тепер дробову частину результату на основу нової системи числення, отримаємо:

А 1 р = а -2 + А 2,

де А 2 - дрібна частина твору,

а -2 - наступна цифра шуканого числа.

Отже, при перекладі вираз (2.2) представляється за схемою Горнера:

А = р -1 (а -1 + р -1 (а -2 + ... + р -1 (а -до + 1 + р -1 а -к) ...)).

Для перекладу правильної дробу з однієї позиційної системи числення в іншу її треба послідовно множити на основу нової системи числення до тих пір, поки в новій дріб не може бути потрібної кількості цифр, яке визначається необхідною точністю уявлення дробу. Правильна дріб в новій системі числення записується з цілих частин творів виходять при послідовному збільшенні, причому перша ціла частина буде старшої цифрою нової дробу.

Розглянемо як приклад переклад правильної дробу 0,536 в двійкову, вісімкову, шістнадцяткову системи числення

10 = 2 = 8 = 16

0,		0,		0,
1,		4,		8,
0,		2,		9,
0,		2,		3,
0,		3,		7,	296
1,		3,
0,		5,	184
0,	608

Переклад дробу в загальному випадку являє собою нескінченний процес. Число цифр в новій системі числення необхідно визначати з умови, що точність представлення числа в новій системі повинна відповідати точності в вихідної системі.

2.3 Переклад неправильних дробів

При перекладі неправильного дробу необхідно окремо перевести цілу і дробову частини по вищевикладених правил і записати число в новій системі числення, залишивши незмінним положення коми.

2.4 Переклад чисел із системи числення в систему з кратним підставою

Якщо підстави систем числення кратні один одному, тобто пов'язані залежністю: l = p m, то кожна цифра системи числення з основою l може бути представлена ​​m цифрами в системі з основою p.

Отже, для того, щоб перевести число з вихідної системи в нову, основа якої кратно основи вихідної системи, досить кожну цифру перекладного числа записати за допомогою m   цифр в новій системі числення, якщо підстава вихідної системи більше підстави нової системи числення. В іншому випадку кожні m   цифр вихідного числа необхідно записати за допомогою однієї цифри в новій системі числення, починаючи для цілих чисел з молодшого розряду і для правильних дробів - зі старшого.

10 = 2 = 8 ; 2 = 16

10 = 2 = 8: 2 = 16

3. Вибір системи числення для застосування в ЕОМ

Очевидно, що непозиційної системи числення непридатні для застосування в ЕОМ через свою громіздкість і труднощі виконання арифметичних операцій.

З позиційних найбільш зручні однорідні. З точки зору застосування в ЕОМ враховуються такі чинники.

1. Наявність фізичних елементів, здатних зобразити символи системи.

2. Економічність системи, тобто кількість елементів необхідне для подання багаторозрядних чисел.

3. Трудомісткість виконання арифметичних операцій в ЕОМ.

4. Швидкодія обчислювальних систем.

5. Наявність формального математичного апарату для аналізу і синтезу обчислювальних пристроїв.

6. Зручність роботи людини з машиною.

7. Перешкодостійкість кодування цифр на носіях інформації.

Історично склалося так, що для застосування в ЕОМ була обрана двійкова система числення, яка найбільш повно відповідає цим критеріям.

В сучасних універсальних ЕОМ застосовуються як двійкова, так і десяткова системи числення. Причому цифри останньої кодуються двійковими символами, т. Е. Мова йде насправді не про десятковою, а про двійковій-десяткового системі числення. Кожна із зазначених систем має свої переваги і недоліки, а також свої області застосування.

Перевагами двійковій системи числення щодо двійковій-десяткового є:

1) економія близько 20% обладнання;

2) приблизно в 1,5 рази більше високу швидкодію;

3) спрощення логічного побудови і значна економія обладнання в схемах управління і в допоміжних ланцюгах.

Перевагами двійковій-десяткового системи є:

1) відсутність необхідності переведення вихідних даних і результатів розрахунків з однієї системи в іншу;

2) зручність контролю проміжних результатів шляхом виведення їх на індикацію для візуального спостереження;

3) більш широкі можливості для автоматичного контролю через наявність в двійковій-десятковому коді надлишкових комбінацій.

Двійкову систему числення застосовують у великих і середніх ЕОМ, призначених для вирішення науково-технічних завдань, для яких характерний великий обсяг обчислень і порівняно малий обсяг вихідних даних і результатів обчислень. Її також доцільно застосовувати в ЕОМ, призначених для управління технологічними процесами.

Двійковій-десяткову систему числення застосовують для вирішення економічних завдань, які характеризуються великим обсягом вихідних даних, порівняльної простотою і малим об'ємом виконуваних над ними перетворень і великою кількістю результатів обчислень. Цю систему доцільно також застосовувати в калькуляторах, ЕОМ, призначених для інженерних розрахунків, а також в персональних ЕОМ.

4. Двоичная система числення

Під двійковій системою числення розуміється така система, в якій для зображення чисел використовуються два символи, а ваги розрядів змінюються за законом 2 + -к, де до - довільне ціле число. Класичною двійковій системою є система з символами 0, 1. Її виконавчі цифри часто називають бітами. У загальному вигляді всі виконавчі числа представляються у вигляді:

А = Σа і 2 І, (і від -до до n)

Щоб опанувати будь-якою системою числення, треба вміти виконувати в ній арифметичні операції. Арифметичні операції в двійковій системі числення виконуються так само, як і в десятковій відповідно до таблиць порозрядних обчислень.

Додавання в двійковій системі числення проводиться за правилами складання полиномов. Тому при додаванні чисел А і В i-й розряд суми S i і перенесення П i з даного розряду в (i + 1) розряд буде визначатися у відповідності з наступним виразом:

а і + b і + П і-1 = S і + П і + 1

а і	b и	П і-1	S и	П і + 1
0	0	0	0	0
0	1	0	1	0
1	0	0	1	0
1	1	0	0	1
0	0	1	1	0
0	1	1	0	1
1	0	1	0	1
1	1	1	1	1

Таблиця множення двох двійкових чисел повністю визначається двома правилами:

Множення будь-якого числа на нуль дає в результаті нуль,

Множення будь-якого числа на 1 залишає його без зміни, тобто результат дорівнює вихідному числу.

4.1 Навички поводження з двійковими числами

Хоча всі правила виконання операцій в двійковій системі числення дуже прості, але тим не менше при роботі з двійковими числами через відсутність навичок виникають різного роду незручності. Нижче наведені деякі прості прийоми, які дозволяють досить вільно поводитися з двійковими числами.

Таблиця 4.1.

n	0	1	2	3	4	5	6	7	8	9	10	11	12
2 n	1	2	4	8	16	32	64	128	256	512	1024	2048	4096

1. Число 100 ... 00 = 2 n.

Необхідно знати напам'ять десяткові значення чисел, представлених в таблиці 4.1.

2. Число 111 ... 11 = 2 n -1.

3. Необхідно знати напам'ять десяткові значення двійкових чисел від 0 до 31 включно. Ці числа в подальшому будуть називатися "малими числами".

4. Двійкове число

А = а n - k +5 а n - k +4 а n - k +3 а n - k +2 а n - k +1 000 ... 000

   мале число k нулів одно А2 k.

Приклад. 11011000 = 11011х2 3 = 27 х 8 = 216.

двійкове число

А = а n - k +5 а n - k +4 а n - k +3 а n - k +2 а n - k +1 00 ... 00 b 5 b 4 b 3 b 2 b 1 = а х 2 k + b

   мале число a мале число b k розрядів

Приклад. 10110000101 = 1011 х 2 7 + 101 = 11 х 128 + 5 = 1413.

5. Якщо в n- розрядному числі багато одиниць і мало нулів, то для визначення його кількісного еквівалента можна з n розрядного числа, записаного одними одиницями, відняти мале число, в якому розряди зі значенням 1 відповідають розрядам вихідного числа з нульовим значенням і навпаки.

Приклад. 11111101001 відповідає

11111111111 = 2 11 - 1

тобто 11111101001 = 2048 -1 - 10110 = 2047 - 22 = 2025.

6. Читання довічних дробів

   А = 0,000 ... 001 = 2 - n Дріб А = 0,111 ... 111 = 1 - 2 - k.

Двійковий дріб читається за тими ж правилами, що і десяткова: розряди праворуч від коми читаються як ціле число, яке є чисельником; знаменник читається як ціле число, яке є 2 k, причому k - номер молодшого розряду праворуч від коми.

5. Форми подання двійкових чисел у ЕОМ

Машинне подання числа - це уявлення числа в розрядної сітці ЕОМ.

Машинне зображення числа умовно позначають [A].

При цьому А = [A] k A,

де k A - масштабний коефіцієнт, величина якого залежить від форми подання числа в ЕОМ.

Під формою подання числа в ЕОМ розуміють звід правил, що дозволяє встановити взаємне відповідність між записом числа і його кількісним еквівалентом.

Якщо довільне дійсне число А` = [A] k A, то таке число представлено в розрядної сітці машини точно. Якщо А` ≠ [A] k A, то довільне дійсне число може бути представлено в машині наближено або взагалі не може бути представлено. При наближеному поданні дійсне число А` замінюється деяким числом [А], що належить безлічі машинних чисел. Безлічі машинних чисел належать тільки числа, кратні двом, так як будь-які два попарно сусідніх машинних числа відрізняються один від одного на величину 2 - n, де n - кількість розрядів.

А min \u003c| A | \u003cA max

Якщо | A | \u003cA min, таке число називають машинним нулем. Числа, більші ніж A max, не можуть бути представлені. У цьому випадку говорять про переповнення розрядної сітки.

Існує три форми подання чисел в ЕОМ: природна, з фіксованою комою і нормальна (з плаваючою комою).

Природною формою запису числа називається запис числа у вигляді полінома, представленого в скороченому вигляді:

А = а n a n-1 ... a 1 a 0 a --1 a --2 ... a --k

При цьому відлік ваг розрядів ведеться від коми. Кома ставиться на строго визначеному місці - між цілою і дробовою частиною числа. Тому для кожного числа необхідно вказати положення його коми в одному з розрядів коду, тобто в загальному випадку місце положення коми повинно бути передбачено в кожному розряді. Зазвичай таку форму подання використовують в калькуляторах.

Якщо місце коми в розрядної сітці машини заздалегідь фіксовано, то таке подання називається поданням з фіксованою комою (крапкою).

У більшості ЕОМ з фіксованою комою числа, з якими оперує машина, менше одиниці і представлені у вигляді правильних дробів, тобто кому фіксують перед старшим розрядом числа, причому числа, більше одиниці, приводяться до такого виду за допомогою масштабного коефіцієнта К А. Подання чисел у вигляді правильних дробів обумовлено необхідністю зменшити можливість переповнення розрядної сітки машини, т. е. зменшити небезпеку втрати значущих цифр старших розрядів при виконанні арифметичних операцій.

Результат множення ніколи не виходить за межі розрядної сітки, якщо кома розташована перед старшим розрядом. Але в цьому випадку результати складання і розподілу можуть вийти за межі розрядної сітки (при операції додавання - не більше ніж на один розряд).

Можна було б оперувати тільки малими числами, тому що ймовірність переповнення при їх складанні мала. Однак це призводить до зниження точності представлення чисел і точності обчислень. Тому завжди прагнуть використовувати числа, величини яких близькі до максимального значення. Однак при цьому на них накладаються наступні обмеження: 1) абсолютна величина суми двох чисел повинна бути менше одиниці; 2) дільник по абсолютній величині має бути більше діленого.

В осередку машини з фіксованою перед старшим розрядом коми число записується в розрядну сітку у вигляді значущої частини дробу зі своїм знаком, т. Е. Для запису n-значної дробу розрядна сітка повинна містити n + 1 розряд.

Розрядна сітка або формат числа в двійковій системі числення має вигляд:

   кома

знак

2 -1

2 -2

2 -n

Тут n розрядів використовують для зображення цифрової частини числа і 1 - для знака.

Величини чисел, що представляються в машинах з фіксованою перед старшим розрядом коми, лежать в межах:

2 -n ≤ | А | ≤ 1-2 -n

У цьому випадку: | А | min = 0, ... 01 = 2 - n, а | А | max = 0,1 ... 1 = 1-2 -n. (Кома розділяє цілу і дробову частини).

Починаючи з обчислювальних машин 2-го покоління, формати чисел в ЕОМ представляються кратними байту, т. Е. N = 8, або 16, 32.

У всіх розглянутих форматах можуть зображуються числа, які по своїй абсолютній величині менше 1, що спрощує конструкцію, зменшує обсяг обладнання. Недоліком такого уявлення чисел є необхідність виконання трудомісткого розрахунку масштабів в процесі підготовки завдання для вирішення у ЕОМ.

Нерідко кому фіксують після молодшого розряду числа. Тоді всі дані представляються у вигляді цілих чисел. У цьому випадку також необхідно масштабування вихідних даних.

Ваги розрядів в форматі числа, що містить n + 1 розряд (1 знаковий) представлені на малюнку:

знак

2 n-1

2 n -2

2 1

2 0

Окремих розрядів для запису цілої частини числа (0) і коми не виділяється, так як їх становище зумовлено формою записи чисел.

Знак числа зазвичай кодується таким чином: знаку «+» відповідає 0 в знаковому розряді, знаку «-» - 1.

При поданні чисел з фіксованою комою в разі виконання арифметичних дій над довільними числами програміст може прийняти будь-яке умовне положення коми в межах формату. Але при розробці програми він повинен стежити за становищем коми під час обчислень, щоб не виникло переповнення.

Необхідність розрахунку масштабів, необхідність стежити за становищем коми під час обчислень виключаються при поданні чисел з плаваючою комою.

У загальному випадку число можна представити у вигляді добутку цілій степені підстави системи і цифрової частини, що є правильним дробом:

А = p m a = p m Σa i p i-m. (I від -k до n),

де a - мантиса, m - порядок.

Формат числа, представленого у формі з плаваючою комою,   має вигляд:

порядок S + 1разрядов мантиса n + 1 розрядів

В розрядної сітці передбачено наявність розряду для фіксації знака мантиси, який відповідає знаку числа.

Подання числа з плаваючою комою можна проілюструвати на наступному прикладі:

987.54 =10 3 * 0.98754,

987.54 =10 4 * 0.098754,

987.54 =10 5 *0.0098754.

З метою однозначного уявлення будь-якого числа введено поняття "нормалізоване число". Нормалізованим вважається число А , Мантиса якого задовольняє нерівності:

2 -1 ≤ | а | ≤ 1-2 -n

Іншими словами, нормалізованим вважається те число, у якого старший розряд дорівнює 1.

Діапазон уявлення порядку числа лежить в межах:

2 S -1≥ m≥ - (2 S -1).

Звідси випливає, що діапазон представлення чисел для p = 2:

мінімальне число:

і максимальне:

Очевидно, що діапазон представлення чисел в машинах з плаваючою комою значно більше, ніж в машинах з фіксованою комою:

≈=

Зіставляючи між собою дві основні форми подання чисел в ЕОМ, можна прийти до наступних висновків.

Діапазон представлення чисел в машинах з фіксованою комою значно менше, ніж в машинах з плаваючою комою, а точність залежить від величини вихідних чисел. Програмування для машин з фіксованою комою значно складніше, тому що доводиться вводити масштабні коефіцієнти, щоб уникнути переповнення масштабної сітки при виконанні арифметичних операцій.

Однак машини з плаваючою комою конструктивно складніші, так як необхідно вводити додаткове обладнання для виконання операцій над порядками чисел, а також передбачити операцію нормалізації і вирівнювання порядків чисел. Час виконання операцій над числами в машині з плаваючою комою більше, ніж в машині з фіксованою комою, що обумовлено необхідністю роботи з порядками.

Як і при фіксованою комою, тут можливо переповнення розрядної сітки, яке виражається в тому, що результат будь-якої операції має порядок більше допустимого. Це призводить до аварійної ситуації. При виконанні операцій можливе отримання чисел, що мають порядок менше допустимого і нормалізовану мантиссу. Ці числа розглядаються як машинні нулі, так само як і числа, які мають нульову мантиссу і допустимий порядок.

Іноді нормальну форму представлення чисел називають полулогарифмической, так як порядок числа р   виражений в логарифмічній формі.

6. Точність представлення чисел в ЕОМ

При вирішенні різних завдань потрібна різна точність одержуваних результатів. Так, при вирішенні інженерних задач достатня точність до 3-4 десяткових знаків (10-13 довічних), при вирішенні наукових завдань - 5-6 десяткових або 16-20 довічних знаків і при вирішенні особливо точних завдань - до 50 двійкових розрядів.

При обмеженій довжині машинних слів безліч чисел, які можна уявити в машині, є кінцевим. Тому уявлення чисел в ЕОМ, як правило, тягне за собою появу похибок, величина яких залежить як від форми подання чисел, так і від довжини розрядної сітки.

Точність представлення числа характеризується абсолютною і відносною похибками.

Абсолютна похибка - це різниця між істинним значенням величини А і її значенням, отриманим з машинного зображення [А], т. Е.

Усереднена абсолютна похибка подання чисел в машинах з фіксованою комою визначається як середнє арифметичне між мінімально уявленим числом і його мінімальною втратою, т. Е.

У машинах з фіксованою комою абсолютна похибка постійна і дорівнює половині молодшого розряду.

Відносна похибка подання визначається як відношення усередненої абсолютної похибки до самого числа:

.

Так як саме число з фіксованою комою змінюється в межах

,

то і відносна похибка є величиною змінною, мінливої ​​відповідно в межах

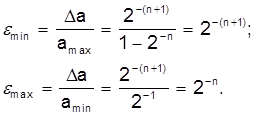
Отже, в машинах з плаваючою комою, на відміну від машини з фіксованою комою, відносна похибка зображення чисел у всьому діапазоні уявлення практично постійна і для чисел з нормалізованої мантиси залежить від кількості розрядів мантиси: чим їх більше, тим менше похибка подання.

У деяких обчислювальних засобах інформаційної одиницею є не окремі числа, а їх блоки або масиви, т. Е. Послідовності, що складаються з сотень і тисяч чисел. У цих випадках нерідко застосовується проміжна форма представлення чисел в ЕОМ, так зване представлення з блоках плаваючою комою, при якому всьому масиву чисел присвоюється загальний порядок і масив вважається нормалізованим, якщо хоча б одне його слово є нормалізованим. Природно, що відносна похибка подання окремих елементів масиву буде при цьому різною. Як і в разі подання з фіксованою комою, максимальний по абсолютній величині елемент буде представлений з мінімальною, в той час як мінімальний по абсолютній величині елемент масиву - з максимальною відносною похибкою. Однак це не має істотного значення, так як основну інформаційне навантаження в цих випадках несуть максимальні елементи масивів. Разом з тим завдяки поданням чисел з блоках плаваючою комою вдається при прийнятної точності обчислень значно скоротити обсяг обладнання, а головне - час виконання операції, так як дії над порядками в цьому випадку виконуються тільки один раз за час обробки всього масиву чисел.

З цього випливає, що не можна віддати перевагу якійсь одній формі представлення чисел. Зазвичай в ЕОМ загального призначення застосовують нормальну форму. Цим забезпечується великий діапазон представлення чисел, висока точність обчислень, простота програмування. Ускладнення апаратури цих ЕОМ має другорядне значення.

У спеціалізованих ЕОМ частіше застосовують фіксовану або по блоках плаваючу кому, якщо інформація обробляється окремими масивами, так як ці форми забезпечують простоту конструкції ЕОМ. Діапазон зміни величин відомий заздалегідь, масштабні коефіцієнти підбираються один раз, необхідна точність обчислень також відома заздалегідь і визначає довжину розрядної сітки.

У сучасних ЕОМ використовуються обидві форми подання чисел. При цьому в більшості випадків формат чисел з фіксованою комою служить для представлення цілих двійкових і десяткових чисел і виконання операцій над ними, що, наприклад, необхідно для операцій над кодами адрес (операції індексного арифметики).

висновок

В процесі написання реферату ми ознайомилися з:

З поняттям системи числення;

Класифікацією систем числення;

Перекладом чисел з однієї системи числення в іншу;

Вибором системи числення для застосування в ЕОМ;

Двійковій системою числення;

Формами представлення двійкових чисел в ЕОМ;

Точністю представлення чисел в ЕОМ і ін.

література

1. Самофалов К.Г., Романкевич А.М., та ін. Прикладна теорія цифрових автоматів. - Київ. "Вища школа" тисячі дев'ятсот вісімдесят сім.

2. Соловйов Г.М. Арифметичні пристрої ЕОМ. - М. "Енергія". 1978.

3. Савельєв А.Я. Прикладна теорія цифрових автоматів - М. "Вища школа". 1987.

4. Каган Б.М. Електронні обчислювальні машини і системи. - М. Вища школа. Тисяча дев'ятсот вісімдесят п'ять.

5. Лисіков Б.Г. Арифметичні і логічні основи цифрових автоматів. - Мінськ. "Вишейшая школа". 1980.