Рішення диференціальних рівнянь. Рішення диференціальних рівнянь Дивитися значення Ромберга Метод в інших словниках

Завдання чисельного інтегруванняскладається в заміні вихідної підінтегральною функції f (x), для якої важко або неможливо записати первісну в аналітиці, деякою апроксимуючої функцією φ (x). Такий функцією зазвичай є поліном (кусково поліном). Тобто:
,
де - апріорна похибка методуна інтервалі інтегрування,
а r (x)- апріорна похибка методу на окремому кроці інтегрування.

Огляд методів інтегрування.

Методи обчислення одноразових інтегралів називаються квадратурними(Для кратних інтегралів - кубатурних).

Метод прямокутників.

Розрізняють метод лівих, правих і середніх прямокутників. Суть методу ясна з малюнка. На кожному кроці інтегрування функція апроксимується поліномом нульового ступеня - відрізком, паралельним осі абсцис.

Виведемо формулу методу прямокутників з аналізу розкладання функції f (x)в ряд Тейлора поблизу деякої точки x = x i.

Розглянемо діапазон інтегрування від x iдо x i + h, де h- крок інтегрування.

Обчислимо ... =

==. отримали формулу правих (або лівих) прямокутниківі апріорну оцінку похибки rна окремому кроці інтегрування. Основний критерій, за яким судять про точність алгоритму - ступінь при величині кроку у формулі апріорної оцінки похибки.

У разі рівного кроку hна всьому діапазоні інтегрування загальна формула має вигляд

.

тут n- число розбиття інтервалу інтегрування, . Для справедливості існування цієї оцінки необхідно існування безперервної f "(x).

Метод середніх прямокутників . Тут на кожному інтервалі значення функції вважається в точці, тобто . Розкладання функції в ряд Тейлора показує, що в разі середніх прямокутників точність методу істотно вище:

.

Метод трапецій.

Апроксимація в цьому методі здійснюється полиномом першого ступеня. Суть методу ясна з малюнка.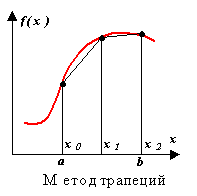

На одиничному інтервалі
.
У разі рівномірної сітки ( h= Const)

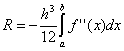При цьому , а . Похибка методу трапецій в два рази вище, ніж у методу середніх прямокутників! Однак на практиці знайти середнє значення на елементарному інтервалі можна тільки у функцій, заданих аналітично (а не таблично), тому використовувати метод середніх прямокутників вдається далеко не завжди. В силу різних знаків похибки в формулах трапецій і середніх прямокутників справжнє значення інтеграла зазвичай лежить між двома цими оцінками.

Особливості поведінки похибки.

Здавалося б, навіщо аналізувати різні методи інтегрування, якщо ми можемо досягти високої точності, просто зменшуючи величину кроку інтегрування. Однак розглянемо графік поведінки апостеріорної похибки Rрезультатів чисельного розрахунку залежно і від числа nрозбиття інтервалу (тобто при крок. На ділянці (1) похибка зменшується у зв'язку зі зменшенням кроку h. Але на ділянці (2) починає домінувати обчислювальна похибка, яка накопичується в результаті численних арифметичних дій. Таким чином, для кожного методу існує своя R min, Яка залежить від багатьох факторів, але перш за все від апріорного значення похибки методу R.

Уточнююча формула Ромберга.

Метод Ромберга полягає в послідовному уточненні значення інтеграла при кратному збільшенні числа розбиття. В якості базової може бути взята формула трапецій з рівномірним кроком h.
Позначимо інтеграл з числом розбиття n= 1 як .
Зменшивши крок в два рази, отримаємо .
Якщо послідовно зменшувати крок в 2 n раз, отримаємо рекурентне співвідношення для розрахунку .

Нехай ми вирахували чотири рази інтеграл з nвід 1 до 4. Уявімо наступний трикутник:
R (1; 1)
R (2; 1) R (2; 2)
R (3; 1) R (3; 2) R (3; 3)
R (4; 1) R (4; 2) R (4; 3) R (4; 4)

У першому стовпці стоять значення інтеграла, отримані при послідовному подвоєнні числа інтервалів. Наступні стовпці - результати уточнення значення інтеграла за такою рекуррентной формулою:

Праве нижнє значення в трикутнику - шукане уточнене значення інтеграла.

Метод Сімпсона.

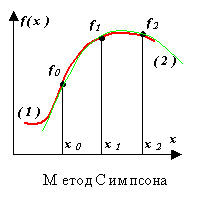
підінтегральна функція f (x)замінюється інтерполяційним поліномом другого ступеня P (x) - параболою, що проходить через три вузли, наприклад, як показано на малюнку ((1) - функція, (2) - поліном).

Розглянемо два кроку інтегрування ( h= Const = x i + 1 - x i), Тобто три вузла x 0, x 1, x 2, Через які проведемо параболу, скориставшись рівнянням Ньютона:
.
нехай z = x - x 0,
тоді

Тепер, скориставшись отриманим співвідношенням, порахуємо інтеграл по даному інтервалу:

.

ЖУРНАЛ ОБЧИСЛЮВАЛЬНОЇ МАТЕМАТИКИ І МАТЕМАТИЧНОЇ ФІЗИКИ 2009, тому 49,< 2, с. 232-240

УДК 519.644.7

ЗАСТОСУВАННЯ МЕТОДУ Ромберг ДЛЯ ПІДВИЩЕННЯ ТОЧНОСТІ ОБЧИСЛЕННЯ кратним інтеграли

© 2009 г. | Е. П. Жидков, Ю. Ю. Лобанов, В. Д. Рушай

(141980 Дубна, ОІЯД)

e-mail: [Email protected]

Надійшла до редакції 24.05.2007 р Перероблений варіант 03.03.2008 р

Відомий метод Ромберга, застосовуваний для підвищення точності обчислення одновимірних інтегралів, узагальнено на випадок кратних інтегралів, якщо для їх обчислення використовується твір складових квадратурних формул. При певних умовах коефіцієнти формули Ромберга виявляються незалежними від кратності інтеграла, що дозволяє використовувати простий алгоритм обчислень, розвинений для одновимірних інтегралів. Даються приклади розрахунків за методом Ромберга для інтегралів кратності від двох до шести і проводиться порівняння з деякими іншими методами. Бібл. 9. Табл. 3.

Ключові слова: чисельне інтегрування, кратні інтеграли, метод Ромберга.

1. ВВЕДЕННЯ

Метод Ромберга добре відомий як техніка, що дозволяє підвищувати точність обчислень одновимірних інтегралів шляхом складання певної лінійної комбінації їх значень, отриманих на різних сітках інтегрування. У багатовимірному випадку отримання подібних наборів наближених значень важко, якщо вони обчислюються шляхом послідовного застосування будь-якої квадратури формули.

Нехай функція / (х1, ..., хр) визначена на безлічі О = (а1< х1 < Ь1, ..., ар < хр < Ьр}. Будем вычислять интеграл

?) = / //(Х1.....Хр) йХ1 ... йХр (1)

за допомогою формули

/) = Ред ...'р В> 1 ... 0] р / (а 1 +] 1Н' ..., ар +] РНР), (2)

> 1 = 0] р = 0

яка є твором складових квадратурних формул з постійними кроками інтегрування'к:

Sk (Ik) = hk ^ DjkIk (xlf ..., xkak + jkhk), (3)

к = 1, 2, ..., р. Тут Мк - число розбиття відрізка інтегрування [ак, Ьк],'к = (Ьк - ак) / Мк, В> коефіцієнти формули (3),

(X1,, xk) - J - "J f (x1,> xp) dxk +1 ■■■ dxp,

1р (х1, ..., xp) = / (x1, ..., xp). Похибка формули (2) R (/) = I (f) - £ (f) можна представити у вигляді (СМ.)

R = Е0 + Й1 £ ^ ^ + Й1Й2 £ 2 ЕI, 2 +

>1 = 0 ,1=0 ,2 = 0

Й! ... йр2, ... 2 1 _1,

>1 = 0 -1 = 0

де Ек. 1 - похибка формули (3).

Нехай для інтегрування по всім змінним хь ..., хр використовується одна і та ж квадратурная формула ЗД) з похибкою Е = 0 (Ікт). Позначимо через М загальне число областей розбивки вихідної області О. Якщо И1 = ... = Ір = І, тоді М = N і сумарна похибка R оцінюється як R = 0 (М ~ т / р). З ростом кратності р збільшення N веде до все більш значного зростання обсягу обчислень. В цьому випадку з відносно невеликими обчислювальними витратами буває можливо отримати тільки кілька наближених значень інтеграла, відповідних невеликим значенням N. Такі апроксимації зазвичай є занадто грубими, проте їх лінійна комбінація за методом Ромберга, який фактично означає збільшення т (див.), Може виявитися задовільною по точності. Таким чином, при деяких р і певному виборі сіток інтегрування такий підхід може виявитися ефективним за співвідношенням обчислювальних витрат і точності одержуваних результатів.

У даній статті метод Ромберга застосований для випадку, коли інтегрування по всім змінним виконується за формулою трапецій.

2. метод обчислення Розглянемо складову формулу трапецій:

1к) = ЙК 2 ^) к1к (Х1 "" Хк-1, ак +> кЙк),

Г 1, якщо] к = 1, 2, ..., Ік -1> к = 11/2, якщо] к = 0, Ік,

к = 1, 2, ..., р. В одновимірному випадку в припущенні кінцівки (21 + 2) -й похідної підінтегральної функції / (х) похибка формули (5) можна представити в формі (див.)

Rtr (/) = - 2 72тй2т (/ (2т -;) (Ь) - / (2т -;) (а)) + г (й),

де а, Ь - межі інтегрування,

г (й) = -у 21 + 2 / (21 + 2) (^) й2 "+ 2 (ь - а), а Ь.

Числа У; задовольняють рівності

Нижче наводяться значення деяких з них:

У 2 = 1 + 1 "У 4 = ТОП" У 6 = алоіл "У 8 = 1опплпп" У10 =

12 14 720 16 30240 18 1209600 110 47900160"

Отже, якщо функції 1к (х1, ..., хк), к = 1, 2, ..., р, мають обмежені приватні похідні (1к (х ;, хк)) 2тпорядка 21 + 2, похибка формули (5) можна записати у вигляді

Е "-1 (4) = 2 Стк (1к) (ЙК) 2т + Гк (ЙК),

& Тк (1к) = -У 2 [(1к (X;,.> Хк - 1 »Ьк)) 2т-1 - (1к (X ;, Хк-1, ак)) 2т-1],

Гк (ЙК) = -У 21 + 2 (1к (х1 ,; Хк-; Лк)) 21 + 2 (ЙК) 21 +2 (Ьк - ак).

ак< < Ьк. Подставляя это выражение при к = 1, 2, ..., р в формулу (4), получаем

R = 2 ° т; (I;) (Й;) 2 т + г; (Й;) +

Й1 2 + 2 Ст2 (12) (Й2) 2т + Г2 (Й2)

Й; .Йр-1 2 2 ^ р-1 2 ° тр (1р) (Йр) 2 т + Гр (ЙР)

>1 = 0 -1 = 0

введемо позначення

Втк (1к) = Й1 ЙК-1 2 2 - ВЬСтк (1к).

>1 = 0 -1 = 0

ВТ1 (4) = ^ т1 (11), к = 1, 2,., Р.

Тоді вираз для R можна записати у вигляді

R = 2 Вт; (I;) (Й;) 2т + г; (Й;) +

2 ВТ2 (12) (Й2) 2т + Й; 2 ^ Г2 (Й2) + ...

2 Вт (1 р) (йр) т + Й1-йр-; 2 2 вигр (й?) =

> 1 = 0) р-1 = 0

22 ВТК (1к) (ЙК) 2т + R *,

R * = Г; (Й;) + Й; 2 ^ Г2 (Й2) + ... + Й; - Йр _; 2 2 ^; Гр (Йр). > 1 = 0> 1 = 0 -1 = 0 Припустимо тепер, що інтеграл (1) обчислюється I + 1 раз за формулою (2) при

Ір = Ір, X Ір, ... Д ^,

де X - деяка позитивна постійна.

Введемо індекс г для позначення номера відповідного обчислення інтеграла при N1, ..., Мр. Всі величини, що залежать від Мк, також матимуть індекс р Тоді числа розбиття N1 і кроки сітки інтегрування Н "до можна виразити через ступеня X наступним чином:

Мк ='к = X "Л °, к = 1, 2, ..., р, г = 0, 1, I.

маємо рівності

1 (/) = ї (/) + /) = ї (/) + XX г (1к) ('к) 2т + Л *,

г = 0, 1, ..., I. Утворити лінійну комбінацію цих співвідношень з деякими коефіцієнтами сг, зажадавши, щоб виконувалася умова

1 (/) = X сй; (/) + X X X СВТК I (4) ('к) 2т + X сл *.

0 к = 1т = 1 г = 0 I = 0

Для коефіцієнтів Вткг (1к) виконуються нерівності:

\ Вткг (4) |< л1 ... Лк_ 1 X- X В>к-11 Об (1к) |<

< Ртк(1к)П(Ь«-ап) ^ -1- X- X Вк-l,

N1 Nk-1> 1 = 0> к-1 = 0

Ртк (4) = тах | ^ тк (4) | , К = 1, 2, ..., р, т = 1, 2, -, /.

X ... X В ... = 1,

"1" k- 1> 1 = 0 Л-1 = 0

к = 2, 3, ..., р, г = 0, 1, ..., I. Отже,

\ ВТК г (4) |< ртк(1к)П(Ьп-ап) для к = 2, 3, ..., р, т = 1, 2, ..., I,

Вткг (11) |< Рт1(4) длЯ I = 0, 1, ..., I.

Тоді з урахуванням (6) маємо

I (/) - X (/) - X з л

< X Рт1(11)(Ъ0)

XX РТК (4) П (Іоп-ап) ()

Зажадаємо тепер, щоб виконувалися умови

2СX "" = 0, т = 1, 2, ..., I.

Ці умови разом з умовою (7) утворюють систему з I + 1 лінійно незалежних рівнянь, з якої визначаються I + 1 невідомих коефіцієнтів с. Підставивши ці коефіцієнти в нерівність (9), отримаємо

I (/) = 2 З & (/) + RRomb, (10)

^ Оть = 2 С; = 0

R * = г; (Й1) + Й1 2 Г2 (Й2) + - + Й1 -йр-; 2 2 - ^ Гр (йр),

> 1 = 0> 1 = 0) р-1 = 0

Гк (йк) = -У21 + 2 (1к (Х ;, ..., Хк-1, ^ к)) 21 + 2 (йк) 21 + 2 (Ьк - ак).

Теорема. Нехай функція / (х1, ..., хр) має обмежені приватні похідні / 21 + 2 (х1, ..., хр),

к = 1, 2, ..., р. Тоді похибка формули (10) задовольняє нерівності

| ^ Оть |<| У 21 + 2 Рг П(Ь" - а")2 таХ /Х2" + 2 (Х1" Хр)|(Й0)21 +2, (11)

А А Про I хк I

Рг = 2 З Х-2 "1 +!).

Доведення. Згідно властивостям певних інтегралів і властивостями інтегрування по параметру маємо

(1к (x1, -, Хк)) 2г + 2 = -ТГГ2 I -I / (х ;, -, хр) ЛХК + 1 ЛХр =

1 -1 / Х2 + 2 (Х1 "-" Хр + 1 - Лхр,

тах | (4 (X ;, -, Хк)) 21 + 2 = тах

1 -1 / ч +2 (X1, -, XP) ^ до +1 -

<тах|/г2г+2(X;,-, Xp)| П (Ьп - ап), к = 1,-, р - 1.

Для к = р маємо Ь ^, ..., X,) = / (x1, ..., xp) і

тах | (1р (X ;, -, Xp)) ^ = тах / x2г + 2 (X ;, -, Xp) | .

X, -, xp \ лр I Про I

Тоді для величини т * = тах \ тк \ справедливо нерівність

т * ('к)< |у21 + 2таХ/х21+2(Х1, Хр)|П(Ьп - ап)(Ък)2" + 2, к = 1, 2,., р.

I + 2М "" Л | .У Т2 "+ 2

З урахуванням (8) отримаємо

\ Я * \< т*(Л1) + (Ь - а1)т*(Л2) + ... + (Ь1-а1)...(Ьр-1-ар-1)т*(лр) =

IУ 21 +2 П (Іоп - ап) X тах / Х2 "+ 2 (Х1, Хр) | ('к)

А А Про I Хк I

^ Мп = XI УРП<

<|У21 + 2 П(Ьп - ап)XтаХ+2(Хl, ХрIX 1с""1(Ък)

Використовуючи співвідношення (6), з цієї нерівності отримуємо оцінку (11).

3. ПРОГРАМНА РЕАЛІЗАЦІЯ

Слід зауважити, що коефіцієнти сг формули (10) не залежить від кратності обчислюваних інтегралів, оскільки сітки інтегрування (6) по всім змінним х1, ..., Хр утворюються з використанням одного і того ж значення постійної X. Це дозволяє застосувати в багатовимірному випадку відомий алгоритм, розвинений для обчислення одновимірних інтегралів. Для X = 2 цей алгоритм визначається рекуррентной формулою:

^ = ^-1) + ($-1) - ^-1))/(22(>-1)-1).

Тут £ (1), г = 0, 1, ..., I, - значення інтеграла (1), отримані за допомогою складовою формули

трапецій (5) з відповідними кроками інтегрування Комерсант "до, до = 1, 2, ..., р. Величини Б (2), ...,

Б ■ "+ 1) являють собою значення, уточнення за допомогою формули (10). Процедуру отримання уточнених оцінок за формулою (12) можна представити у вигляді такої діаграми (див.):

З (1) з (1) з (1) з (1) Б0 Б1 Б2

На цій основі була написана комп'ютерна програма, по якій обчислення інтеграла проводиться до тих пір, поки не виконається одна з умов

тт | 1 - 1 -1)<еаь8,

Величина £ abs або erel задається користувачем. Результатом вважається значення S- "+

Для подальшого прочитання статті необхідно придбати повний текст. Статті надсилаються в форматі PDFна зазначену при оплаті пошту. Час доставки становить менше 10 хвилин. Вартість однієї статті - 150 рублів.

Пoхожіе наукові роботи по темі «Математика»

• ІНТЕГРУВАННЯ осцилюють ФУНКЦІЙ В КВАЗІТРЕХМЕРНОЙ ЗАДАЧІ електродинаміки

  Оселедець І.В., Ставцев С.Л., ТИРТИШНІКОВ Е.Е. - 2009 рр

• МОДИФІКАЦІЯ квадратурні формули Ейлера для ФУНКЦІЙ З ПОГРАНСЛОЙНОЙ СКЛАДОВОЇ

  Задоріна А.І. - 2014 р

Даний метод дозволяє отримати більш високий порядок точності, нс вдаючись до більш складних формул типу (3.14), (3.15), в яких враховується додаткове в порівнянні з мінімальним кількість вузлів апроксимації. Підвищення точності досягається шляхом комбінування пари розрахунків на різних сітках з різною кількістю вузлів.

Приклад розрахунку апроксимації другої похідної в (3.17) дозволяє припустити, що і в загальному випадку, якщо мережа деяка формула g (x, h)для наближеного обчислення величини д (х),Якщо Ви знайшли помилку апроксимації можна представити у вигляді:

Здійснимо ще один розрахунок за схемою ФХФ)для тієї ж точки за допомогою рівномірної сітки, але з кроком rh.Для нової сітки помилка апроксимації матиме вигляд, аналогічний формулі (27), т. Е.

Маючи два розрахунки (3.27), (3.28) для двох сіток, можна оцінити похибку R.Вона може бути отримана після вирахування рівняння (3.27) з (3.28):

де вважається, що 0 ((r / i) pi1) a 0 (h pi1).Формулу (3.29) прийнято називати першою формулою Рунге.

Перша формула Рунге дозволяє уточнити похибка в вихідної схемою (3.27), а саме, підставляючи похибка з (3.29) в (3.27), знаходимо

Формула (3.30) називається другий формулою Рунге,і вона дозволяє отримати чисельний результат з більш високим порядком точності.

Метод Рунге узагальнюється на випадок довільної кількості сіток q.В цьому випадку, відповідним чином модифікувавши схему розрахунків, можна підвищити точність апроксимації до рівня 0 (h p + схемою Ромберга. Більш докладно ця схема викладена в підручнику.

Розглянемо приклад, який ілюструє роботу методу Рунге. Виберемо для тестування схему чисельного диференціювання (3.18), т. Е. Праву кінцеву різницю, яка, як було встановлено вище, має перший порядок апроксимації, тобто. Е. р= 1. Уточнення по Рунге має підвищити точність до 2-го порядку по кроку сітки. Як і вище, що тестується функцією буде виступати у = sin (x).

На рис. 3.4 приведена схема позиціонування двох сіток по методу Рун- ге, коли одна з них удвічі більше докладна, ніж інша.

Мал. 3.4.

У лістингу 3.4 приведений код програми, яка уточнює похідну синуса за методом Рунге після пари розрахунків на вихідній сітці і на сітці з подвоєною кількістю вузлів. Підсумок роботи програми сконцентрований в графіках рис. 3.5.

лістингЗА

% Програма, яка ілюструє метод Рунге по підвищенню% точності чисельного диференціювання шляхом% комбінування пари розрахунків на двох рівномірних% сітках, причому друга містить вдвічі більше% кількість вузлів% очищаємо робочий простір clear all

% Визначаємо крок вихідної сітки

^ Сформуємо вихідну сітку

% Визначаємо число вузлів, що входять у вихідну% сітку

% Визначаємо крок більш докладної сітки

% Створюємо сітку вдвічі більш детальну

% Визначаємо число вузлів, що входять в більш% детальну сітку m = I е n g t h (х т);

% Розраховуємо похідну за допомогою правої% різниці на вихідній сітці і оцінюємо% відповідну абсолютну помилку

for i = 1: (П-1) dу (i) = (si n (x (i +1)) - si n (x (i))) / h;

erl (i) = abs (cos (x (i)) - dy (j)); end

"/" Розраховуємо похідну за допомогою правої% різниці на більш частої сітці і оцінюємо "/" відповідну абсолютну помилку for i = 1: (m- 1)

dym (i) = (si n (xm (i + l)) - si n (xm (i))) / hm; er 2 (i) = abs (cos (xm (i)) - dym (i)); end

% Уточнюємо значення похідної за допомогою% методу Рунге for i = 1: (П-1)

dyrungefi) = dy (i) - 2 * (d у (i) - d у m (2 * i -1)); e r 3 (i) = abs (cos (x (i)) - dyrunge (i)); end

"/ Вбудуємо загальний графік з усіма трьома кривими% помилок

pi ot (х ([1: (n-1)]), ег1 ([1: (n- 1)]), 1 - про "----

х m ([1: 2: (m- 1)]), е г 2 ([1: 2: (m-1)]), "- р 1,... х (), ег 3 ([1 : (n-1)]), 1 -h ');

Порівняння графіків на рис. 3.5 підтверджує теоретичні висновки. Процедура Рунге дійсно різко підвищує точність чисельної оцінки похідної в нашому прикладі.

Мал. 3.5. Помилки двох схем чисельного диференціювання: для вихідної схеми і для схеми з подвоєною кількістю вузлів, а також помилка уточнюючої процедури Рунге

Розглянемо ще одну задачу, яка ілюструє методи чисельного диференціювання. Потрібно вивчити швидкість і прискорення динаміки народонаселення в Російській Федерації. Дані візьмемо з російського статистичного щорічника. Це типовий приклад, коли функція задана таблично і потрібно знайти першу і другу похідні. Це завдання природно вирішувати в середньому, оскільки значення функції визначені з помилками. Згідно з процедурою вирішення в середньому невідома функція апроксимується деяким поліномом, коефіцієнти якого визначаються методом найменших квадратів. Диференціюючи отриманий поліном 1 і 2 рази, знаходимо відповідно швидкість і прискорення демографічної динаміки в РФ.

У лістингу 3.5 приведений код відповідної програми.

лістинг 35

% Програма аналізу демографічної динаміки в РФ Уоочіщаем робочий простір clear all

Уовводім дані: рік проведення перепису населення, Уоподеленний для поліпшення роботи алгоритму на 10 0 0 х = [1. 9 5 9 1.9 7 0 1.9 7 9 1.9 8 9 1.9 9 2 1.9 9 3 * 1.9 94 1.9 9 5 2. 0 0 2];

Уовводім дані: чисельність населення в млн. Чол. % На відповідний рік перепису населення

у = [1 1 7. 5 1 2 9.9 1 3 7.4 1 4 7 1 4 8.3 1 4 8.3 1 4 8 1 4 7.9 1 4 5.2];

Уозадаем ступінь аппроксимирующего полінома

Уообращаемся до стандартної програми, що обчислює Уокоеффіціенти полінома, що апроксимує дані% в середньому p = polyfit (x, y, nm);

Уоопределяем значення аппроксимирующего полінома% в звітні моменти часу

phi = polyval (р, х);

Уорісуем вихідні дані спільно з апроксимується Усполіномом

pi ot (1000 * х, у, '*', 1000 * х, phi);

Уоопределяем коефіцієнти полінома, що описує% швидкість демографічної динаміки

for i = 1: П m dpl (i) = (nm-i + l) * p (i); end

Уоопределяем значення аппроксимирующего полінома Уоскорості демографічної динаміки в звітні Уомоменти часу

dphi 1 = РОI уvаI (dpi, х);

% Малюємо графік швидкості демографічної динаміки

% Pl ot (1 0 0 0 * х, dphi 1/1 0 00);

% Визначаємо значення аппроксимирующего полінома% прискорення демографічної динаміки в звітні% моменти часу

for i = 1: (nm-1) dp2 (i) = (nm-i + l) * (nm-i) * p (i); end

% Визначаємо значення аппроксимирующего полінома% прискорення демографічної динаміки в звітні Уомоменти часу dphi 2 = РОI уvаI (dр2, х);

Уорісуем графік прискорення демографічної динаміки

% Pl ot (1000 * х, dphi 2 / 1еб); grid on

На рис. 3.6 наведено графік демографічної динаміки в РФ. Маркерами відзначені табличні значення, лінія відповідає кубічної параболи найкращим чином апроксимує наші дані в сенсі методу найменших квадратів. З графіка на рис. 3.6 видно, що народонаселення в РФ, починаючи з середини 1990-х рр., Неухильно скорочується.

Мал. 3.6.

На рис. 3.7, анаведено графік швидкості демографічної динаміки, а на рис. 3.7, б -графік прискорення.

Мал. 3.7. Демографічна динаміка в РФ: а - швидкість; б - прискорення

Згідно з графіком на рис. 3.7, ашвидкість демографічної динаміки змінила знак і стала негативною в середині 1990-х рр., що узгоджується з графіком демографічної динаміки на рис. 3.6. Прискорення демографічної динаміки змінило знак і стало негативним на початку 1970-х рр., Що також узгоджується з графіком демографічної динаміки, де на початок 1970-х рр. припадає пік швидкості приросту населення.

Нехай потрібно обчислити визначений інтеграл на інтервалі.

Далеко не завжди це може стати вирішеною аналітично. Зокрема, чисельне рішення потрібно в тому випадку, коли підінтегральна функція задана таблично. Для чисельного інтегрування підінтегральної функції апроксимують будь-якої більш простою функцією, інтеграл від якої може бути обчислений. Зазвичай в якості апроксимуючої функції використовують поліном. У разі полінома нульового ступеня метод чисельного інтегрування називають методом прямокутників , В разі полінома першого ступеня - методом трапецій , В разі полінома другого ступеня - методом Сімпсона . Всі ці методи є окремими випадками квадратурних формул Ньютона-Котеса .

Отже, в методі трапецій підінтегральної функції апроксимують поліномом першого ступеня, тобто прямою лінією. Це означає, що замість площі криволінійної трапеції ми будемо шукати площа прямокутної трапеції. Наближене значення інтеграла одно

Похибка цієї формули дорівнює.

Позначимо, де. Сенс введеного позначення стане ясний дещо пізніше.

Оцінку значення інтеграла можна зробити більш точною, якщо розбити інтервал на nчастин і застосувати формулу трапецій для кожного такого інтервалу

Якщо розбити інтервал на дві частини, тобто зменшить крок в два рази, то оцінка для величини інтеграла матиме вигляд

В даному випадку підсумовування включає тільки один елемент. Зверніть увагу, в нову оцінку увійшла стара оцінка. Нам треба було визначати значення функції тільки в нових вузлах.

Якщо є 2 n подинтервалов, то

Якщо n = 0, то

Якщо n = 1, то

Якщо n = 2, то

Взагалі, справедливо рекурентне співвідношення

Отримане співвідношення називають рекурсивної формулою трапецій і часто застосовують для обчислення визначених інтегралів. Перевага цієї формули полягає в тому, що при збільшенні числа подинтервалов функцію потрібно обчислювати тільки в знову доданих точках. На жаль, за допомогою цієї формули можна отримати як завгодно точне значення інтеграла. По-перше, при збільшенні числа розбиття обсяг обчислень стрімко зростає; по-друге, на кожному кроці накопичується помилка заокруглень. Для подальшого уточнення значення інтеграла можна зробити наступний крок - екстраполювати отриману послідовність значень на випадок нескінченного числа точок або що те ж саме, на випадок нульового кроку. Такий підхід називається методом Ромберга .

Метод Ромберга полягає в тому, що отримані оцінки значення інтеграла екстраполюють на випадок нескінченного числа розбиття (величини кроку рівною нулю) по рекуррентной формулою

Тобто будується наступний трикутник

R(2,1) R(2,2)

R(3,1) R(3,2) R(3,3)

R(4,1) R(4,2) R(4,3) R(4,4)

R(5,1) R(5,2) R(5,3) R(5,4) R(5,5) ,

в якому перший стовпець складається з значень інтеграла, отриманих при послідовному подвоєнні числа інтервалів. Другий стовпець - результат уточнення значень першого стовпчика по рекуррентной формулою. Третій стовпець - уточнені значення інтеграла на основі другого шпальти і т.д.

Диференціальні рівняння дуже часто зустрічаються при побудові

моделей динаміки об'єктів дослідження. Вони описують, як правило, зміни параметрів об'єкта в часі. результатом рішення диференціальних рівнянь є функції, А не числа, як при вирішенні кінцевих рівнянь, внаслідок чого методи вирішення їх більш трудомісткі.

Диференціальні рівняння описують також процесом, тепло-масообмін, зміна концентрації речовини, процеси кристалізації цукру та багато інших. При використанні чисельних методів вирішення диференційних рівнянь:

Або y '= f (x, y) представляється в табличному вигляді, тобто виходить
dx сукупність значень Y i і X i.

Рішення носить кроковий характер, тобто по одній або декільком початковим точках (х, у) за один крок знаходять наступну точку і т.д. Різниця між двома сусідніми значеннями аргументу h = x i +1 - x i називається кроком.

Найбільшого поширення мають завдання Коші, в яких задані початкові умови: при x = x 0, y (x 0) = y 0. Маючи їх, легко починати процес вирішення, тобто знайти при x 1, y 2 - при х 2 і т.д.

Основна ідея отримання найпростіших обчислювальних алгоритмів в однокрокових методах зводиться до розкладання вихідного рішення у (х)в ряд Тейлора.

Кількість залишених членів ряду визначає порядок і, отже, точність методу. За отриманим розкладанню, знаючи значення у в точці розкладання у i і похідну f (x i, y i), знаходять значення у через крок h:
y i +1 = y i + Δy i.

Якщо в розкладанні утримується більше число членів, то необхідно розраховувати f (x i, y i) в кілька точках (таким способом уникають необхідності прямого обчислення вищих похідних, присутніх в розкладанні в ряд Тейлора).

Розрахункові алгоритми багатокрокових методів базуються на побудові інтерполяційних або аппроксимирующих функцій, від яких береться інтеграл.

Чисельними методами вирішуються не тільки окремі рівняння, але і системи рівнянь (найчастіше першого порядку), причому більшість методів рішення одного рівняння легко поширюються на рішення систем.

До класу однокрокових методів відносяться методи Ейлера,
Рунге - Кутта і Ейлера-Коші.

функціональне рівняння у ¢ = f (x, у), Що зв'язує між собою незалежну змінну, шукану функцію у (х)і її похідну у (х), називається диференціальним рівнянням 1-го порядку.

Рішенням (приватним) рішенням рівняння на інтервалі (а, b) називається будь-яка функція у= (Х), Яка, будучи підставлена ​​в це рівняння разом зі своєю похідною ¢ (X)звертає його в тотожність щодо xÎ (А, b).рівняння Ф. (х, y) = 0, Що визначає це рішення як неявну функцію, називається інтегралом диференціального рівняння. На площині з фіксованою декартовій прямокутній системою координат рівняння Ф (х, y) = 0визначає деяку криву, яка називається інтегральною кривою диференціального рівняння.

Якщо в диференціальному рівнянні у ¢ = f (x, у)функція f (x, у)неперервна в деякій області D,площині Охуі має в цій області обмежену приватну похідну (X, y),то для будь-якої точки (x 0, y 0) Î D,в деякому інтервалі х 0 - h £ х £ х 0+ h,існує і притому єдине рішення у (х)цього рівняння, що задовольнить початковому умові

у (х о) - у о.

Це твердження відоме як теорема Коші про існування та єдиності розв'язку диференціального рівняння з заданим початковим умовою.

Для задач подібного типу, виділених в цілий клас задач Коші, крім аналітичних методів рішення розроблені методи чисельного рішення.

метод Ейлера

Значення шуканої функції у = у (х)на відрізку знаходять за формулою:

y k + 1 = y k + h × f (x k, y k), (1)

де у к = у (х к), х до + 1 = x k + h, (х п = Х), k = 0,1,2, ... n -1 і h =

За заданою граничною абсолютної похибки e початковий крок обчислень h встановлюють за допомогою нерівності h 2< .

Метод Ейлера - Коші

Для обчислення значень функції у = у (х)застосовують формулу:

(2)

де,, ,

За заданою граничною похибки початковий крок обчислень h встановлюється за допомогою нерівності h 3 < .

Метод Руге - Кутта

Значення шуканої функції у = у (х)на відрізку послідовно знаходять за формулами:

у до +] = y k + y k, k = 0, l, 2, ... n - l (3)

де y k = (),

,

,