Послідовності прямокутних імпульсів. Аналіз спектру послідовності прямокутних імпульсів Спектр періодичної послідовності прямокутних імпульсів

Спектральне подання тимчасових функцій широко використовується в теорії зв'язку. Для теоретичних і експериментальних досліджень характеристик електричних ланцюгів і передачі повідомлень по каналах зв'язку використовується різні типи сигналів: гармонійні коливання, рівні постійних напруг, послідовності прямокутних і радіоімпульсів і т. Д. Особливо важливу роль в теоретичних дослідженнях електричних ланцюгів грають обчислювальні сигнали у формі одиничної функції і імпульсної функції (функції Дірака). Визначимо спектри найбільш поширених типових сигналів.

11.1 Спектр послідовності прямокутних імпульсів

Нехай є періодична послідовність імпульсів прямокутної форми періодом Т тривалістю імпульсів t і і амплітудою А. Аналітичне вираження функції, яка описує імпульс на відрізку, має вигляд

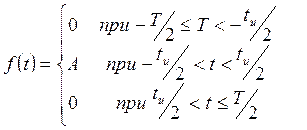(11.1)

Графік періодичної послідовності імпульсів зображений на малюнку 11.1.

малюнок 11.1

Ця функція є парною, так як її графік симетричний відносно осі ординат. Тоді коефіцієнти Фур'є це функції обчислюються за формулами (КФТ2), де.

Число є середнє значення функції за період і називається постійної складової. Частоту називають основною, або першою гармонікою, а частоти k вищими гармоніками, де k \u003d 2,3,4, ...

Побудуємо амплітудний спектр розглянутій послідовності прямокутних імпульсів. Так як функція періодична, то її амплітудний спектр є лінійчатим. Позначимо через відстань між будь-якими сусідніми гармоніками. Очевидно, воно дорівнює. Амплітуда k-ої гармоніки згідно (11.2) має вигляд

(11.3)

Знайдемо відношення між періодом Т і тривалістю імпульсу, при якому амплітуда k-ої гармоніки звертається в нуль.

А 2 ≈32В, А 3 ≈15В, А 4 ≈0, А 5 ≈6,36В, А 6 ≈10,5В, А 7 ≈6,36В, А 8 ≈0, А 9 ≈4,95В, А 10 ≈6,37В.

Отриманий в результаті розрахунку амплітудний спектр наведено на малюнку 11.2.

малюнок 11.2

Такий спектр називають лінійчатим або дискретним спектром.

Аналогічно розраховані і побудовані спектри для q \u003d 8 і q \u003d 16. Вони наведені на малюнках 11.3 і 11.4 відповідно.

малюнок 11.3

малюнок 11.4

З малюнка видно, що чим більше шпаруватість прямокутних імпульсів, тим менше значення має амплітуда першої гармоніки, але тим повільніше убуває спектр.

11.2 Спектр одиночного прямокутного імпульсу

Розглянемо Ф (11.1) для випадку, коли Т → ∞, тобто періодична послідовність імпульсів вироджується в одиночний прямокутний імпульс, тривалістю t u.

Аналітичний вираз для цього імпульсу запишеться у вигляді:

Графік цієї функції зображено на малюнку 11.5.

малюнок 11.5

В цьому випадку частота першої гармоніки і відстань між гармоніками стає рівним 0, отже, спектр з дискретного перетворюється в безперервний, що складається з нескінченно великого числа спектральних ліній, які перебувають на нескінченно малих відстанях один від одного. Такий спектр називають суцільним. Звідси випливає найважливіше правило: періодичні сигнали породжують дискретні спектри, а неперіодичні - суцільні (безперервні).

Спектр прямокутного одиночного імпульсу можна знайти безпосередньо з прямого перетворення Фур'є (10.1)

Розглянемо періодичну послідовність імпульсів прямокутної форми з періодом Т, тривалістю імпульсів t u і максимальним значенням. Знайдемо розкладання в ряд такого сигналу, вибравши початок координат, як показано на рис. 15. При цьому функція симетрична щодо осі ординат, тобто всі коефіцієнти синусоїдальних складових \u003d 0, і потрібно розрахувати тільки коефіцієнти.

постійна складова

(2.28)

Постійна складова - це середнє значення за період, тобто це площа імпульсу, поділена на весь період, тобто , Тобто то ж, що вийшло і при строгому формальному обчисленні (2.28).

Згадаймо, що частота першої гармоніки | 1 \u003d, де Т - період прямокутного сигналу. Відстань між гармоніками D| \u003d | 1. Якщо номер гармоніки n виявиться таким, що аргумент синуса, то амплітуда цієї гармоніки перший раз звертається в нуль. Ця умова виконується при. Номер гармоніки, при якому амплітуда її наближається до нуля перший раз, називають «Першим нулем» і позначають його буквою N, підкреслюючи особливі властивості цієї гармоніки:

З іншого боку, шпаруватість S імпульсів - це відношення періоду Т до тривалості імпульсів t u, тобто . Отже «перший нуль» чисельно дорівнює скважности імпульсу N \u003d S. Оскільки синус звертається в нуль при всіх значеннях аргументу, кратних p, то і амплітуди всіх гармонік з номерами, кратними номером «першого нуля», теж звертаються в нуль. Тобто при, де k - будь-яке ціле число. Так, наприклад, з (2.22) і (2.23) випливає, що спектр прямокутних імпульсів з шпаруватістю 2 складається тільки з непарних гармонік. оскільки S \u003d 2, То і N \u003d 2, Тобто амплітуда другої гармоніки перший раз звертається в нуль - це «перший нуль». Але тоді і амплітуди всіх інших гармонік з номерами, кратними 2, тобто всі парні теж повинні звертатися в нуль. При скважности S \u003d \u200b\u200b3 нульові амплітуди будуть у 3, 6, 9, 12, ... .гармонік.

Зі збільшенням шпаруватості «перший нуль» зміщується в область гармонік з великими номерами і, отже, швидкість убування амплітуд гармонік зменшується. Простий розрахунок амплітуди першої гармоніки при U m\u003d 100В для скважности S=2, U m 1\u003d 63,7B, при S=5, U m 1\u003d 37,4B і при S=10, U m 1\u003d 19,7B, тобто з ростом скважности амплітуда першої гармоніки різко зменшується. Якщо ж знайти відношення амплітуди, наприклад, 5-й гармоніки U m 5 до амплітуди першої гармоніки U m 1, То для S=2, U m 5/U m 1\u003d 0,2, а для S=10, U m 5 / U m 1 \u003d0,9, тобто швидкість загасання вищих гармонік з ростом скважности зменшується.

Таким чином, з ростом скважности спектр послідовності прямокутних імпульсів стає більш рівномірним.

Розглянемо періодичну послідовність імпульсів прямокутної форми з періодом Т, тривалістю імпульсів і максимальним значенням . Знайдемо розкладання в ряд такого сигналу, вибравши початок координат як показано на рис. 15. при цьому функція симетрична щодо осі ординат, тобто всі коефіцієнти синусоїдальних складових \u003d 0, і потрібно розрахувати тільки коефіцієнти .

- 0 T t

постійна складова
(28)

Постійна складова - це середнє значення за період, тобто це площа імпульсу
, Поділена на весь період, тобто
, Тобто то ж, що вийшло і при строгому формальному обчисленні (28).

Згадаймо, що частота першої гармоніки  1 \u003d , Де Т - період прямокутного сигналу. Відстань між гармонікамі \u003d  1. Якщо номер гармоніки n виявиться таким, що аргумент синуса
, звідки . Номер гармоніки, при якому амплітуда її наближається до нуля перший раз, називають «Першим нулем» і позначають його буквою N, підкреслюючи особливі властивості цієї гармоніки:

(29)

з іншого боку, шпаруватість S імпульсів - це відношення періоду Т до тривалості імпульсів t u, тобто . Отже «перший нуль» чисельно дорівнює скважности імпульсу N= S. Оскільки синус звертається в нуль при всіх значеннях аргументу, кратних , то і амплітуди всіх гармонік з номерами, кратними номером «першого нуля», теж звертаються в нуль. Тобто
при
, де k - будь-яке ціле число. Так, наприклад, з (22) і (23) випливає, що спектр прямокутних імпульсів з шпаруватістю 2 складається тільки з непарних гармонік. оскільки S=2 , То і N=2 , Тобто амплітуда другої гармоніки перший раз звертається в нуль - це «перший нуль». Але тоді і амплітуди всіх інших гармонік з номерами, кратними 2, тобто всі парні теж повинні звертатися в нуль. При скважности S \u003d \u200b\u200b3 нульові амплітуди будуть у 3, 6, 9, 12, ... .гармонік.

Зі збільшенням шпаруватості «перший нуль» зміщується в область гармонік з великими номерами і, отже, швидкість убування амплітуд гармонік зменшується. Простий розрахунок амплітуди першої гармоніки при U m \u003d 100В для скважности S=2, U m 1 \u003d 63,7B, при S=5, U m 1 \u003d 37,4B і при S=10, U m 1 \u003d 19,7B, тобто з ростом скважности амплітуда першої гармоніки різко зменшується. Якщо ж знайти відношення амплітуди, наприклад, 5-й гармоніки U m 5 до амплітуди першої гармоніки U m 1 , То для S=2, U m 5 /U m 1 \u003d 0,2, а для S=10, U m 5 / U m 1 = 0,9, тобто швидкість загасання вищих гармонік з ростом скважности зменшується.

Таким чином, з ростом скважности спектр послідовності прямокутних імпульсів стає більш рівномірним.

2.5. Спектри при зменшенні тривалості імпульсу і періоду сигналу.

регулювати шпаруватість S= T/ t n можна або зміною тривалості імпульсу t n при T\u003d Const, або зміною періоду Т при t n \u003d Const. Розглянемо спектри сигналів при цьому.

T \u003d Const,t n \u003d Var. Частота першої гармоніки f 1 =1/ T= const і  f= f 1 = const. перший нуль N= T/ t n і в міру укорочення імпульсу t n зміщується в область гармонік з великими номерами. при t n 0 N, спектр виходить дискретним і  f= f 1 , Нескінченно широкий і з нескінченно малими амплітудами гармонік.

t n \u003d Const,T \u003d Var. Будемо збільшувати період Т, Тоді частота першої гармоніки f 1 і відстань між спектральними лініями  f зменшуватимуться. Так як  f= f 1 \u003d 1 / Т, То спектральні лінії будуть зміщуватися в область більш низьких частот і «щільність» спектра зросте. якщо Т, то сигнал з періодичного стає неперіодичним (одиночний імпульс). В цьому випадку f 1 =  f0, тобто спектр з дискретного перетворюється в безперервний, що складається з нескінченно великого числа спектральних ліній, які перебувають на нескінченно малих відстанях один від одного.

Звідси випливає правило: періодичні сигнали породжують дискретні (лінійчатих) спектри, а неперіодичні - суцільні (безперервні).

При переході від дискретного спектра до безперервного ряд Фур'є замінюється інтегралом Фур'є. Найбільш просто ця заміна виконується, якщо використовувати запис ряду Фур'є в комплексній формі (16) і (17). Інтеграл Фур'є для безперервного спектра записується

, (30)

де
(31)

функція F(j ) називається спектральної функцією або спектральної щільністю, Яка залежить від частоти. Формули (30) і (31) називають в сукупності одностороннім перетворенням Фур'є, Яке є окремим випадком більш загального перетворення Лапласа і виходить заміною в перетворенні Лапласа комплексної змінної р на j .

Спектральну функцію можна представити як огибающую коефіцієнтів ряду Фур'є, тобто як межа лінійного спектра періодичної функції при Т. функція F(j ) може бути дійсною чи комплексної. Вважаючи в загальному випадку
, Ми отримуємо дві частотні характеристики:
-амплітудний спектр, Тобто залежність амплітуди спектральних складових від частоти, і  ( ) – фазовий спектр, Тобто закон зміни фази спектральних складових сигналу від частоти. Можна показати, що амплітудний спектр - завжди парна, а фазовий спектр - завжди непарна функція . Спектральну функцію для багатьох неперіодичних сигналів (одиночних імпульсів різної форми) найбільш легко і просто знаходити за допомогою таблиць оригіналів і зображень в перетворенні Лапласа, які наводяться в навчальній і довідковій літературі. Після знаходження зображення по Лапласа F(p) для заданої неперіодичної функції f(t) , Спектральна функція знаходиться

(32)

Отже, згідно з (30) неперіодичних функція f(t) представляється сукупністю нескінченно великого числа гармонік з нескінченно малими амплітудами
у всьому діапазоні частот від - до + , тобто уявлення f(t) у вигляді інтеграла Фур'є має на увазі підсумовування незатухаючих гармонічних коливань нескінченного суцільного спектра частот.

опис лабораторної установки

Робота виконується на блоці «Синтезатор сигналу», функціональна схема якого приведена на рис. 16.

Блок містить генераторів Г1-Г6 шести перших гармонік сигналу. Частота першої гармоніки дорівнює 10 кГц. Гармонійний сигнал з виходу n-го генератора через фазообертач Ф n і атенюатор А n надходить на суматор. Фазовращателямі задають початкові фази  n гармонік, а аттенюаторами - їх амплітуди А n.

На виході суматора в загальному випадку виходить сума шести гармонік сигналу

.

З виходу суматора сигнал подається на вхід Y осцилографа. Для його зовнішньої синхронізації використовується спеціальний імпульсний сигнал, що подається з гнізда «Синхрон.» на вхід Х осцилографа. Для установки і контролю амплітуд гармонік передбачена можливість відключення будь-який з гармонік. Включивши тільки генератор n-ої гармоніки, можна встановити її амплітуду аттенюатором А n і оцінити її значення за допомогою осцилографа. Кожен фазообертач за допомогою перемикача дозволяє встановити необхідну дискретне значення початкової фази гармоніки, або відключити генератор.

2. Спектр періодичної послідовності прямокутних імпульсів

Розглянемо періодичну послідовність прямокутних імпульсів, зображену на рис. 5. Даний сигнал характеризується тривалістю імпульсу, його амплітудою і періодом. За вертикальної осі відкладається напруга.

Рис.5. Періодична послідовність прямокутних імпульсів

Початок відліку виберемо в середині імпульсу. Тоді сигнал розкладається тільки по косинусам. Частоти гармонік равниn / T, де n- будь-яке ціле число. Амплітуди гармонік згідно (1.2.) Будуть рівні:

так як V (t)=Е при, де - тривалість імпульсу і V (t)\u003d 0 при, то

Цю формулу зручно записати у вигляді:

(2.1.)

Формула (1.5.) Дає залежність амплітуди n-ої гармоніки від періоду і тривалості у вигляді безперервної функції (функція ). Цю функцію називають обвідної спектра. Слід мати на увазі, що фізичний зміст вона має тільки на частотах, де існують відповідні гармоніки. На рис. 6 наведено спектр періодичної послідовності прямокутних імпульсів.

Рис.6. Спектр періодичної послідовності

прямокутних імпульсів.

При побудові обвідної маємо на увазі, що - є

Осцілірующей функцією частоти, а знаменник монотонно зростає з ростом частоти. Тому виходить квазіосцілірующая функція з поступовим спадання. При частоті наближається до нуля, до нуля прагнуть одночасно і чисельник і знаменник, їхнє ставлення прагне до одиниці (перший класичний межа). Нульові значення обвідної виникають в точках де т. Е.

де m - ціле число (крімm

Лабораторна робота №1.

Подання періодичних імпульсних

Сигналів поруч Фур'є.

Мета роботи - Вивчення спектрального складу періодичної послідовності імпульсів прямокутної форми при різних частотах проходження і тривалості імпульсів.

Вступ

Для, передачі зберігання і обробки інформації використовуються періодичні імпульсні сигнали, які можуть бути математично представлені рядами Фур'є. Існує тимчасове рис.1 і частотне представлення електричних сигналів рис.2.

Рис.1. Тимчасова форма подання періодичної

послідовності прямокутних імпульсів.

Подання сигналу у часовій області дозволяє визначити його параметри, енергію, потужність і тривалість. Для подання сигналів в частотній області у вигляді спектра використовується перетворення Фур'є. Знання частотних властивостей дозволяє вирішувати задачі ідентифікації характеристик сигналу (визначення його найбільш інформативних параметрів), фільтрації (виділення корисного сигналу на тлі перешкод), вибору частоти дискретизації безперервного сигналу. Одним з найважливіших параметрів сигналу є ширина частотного спектра, т. К. Саме цей параметр виявляється визначальним при узгодженні сигналу з апаратурою обробки і передачі інформації.

Основні формули і визначення.

періодичну функцію u (t)з періодом T можна уявити поруч Фур'є

(1)

коливання з частотою називається першою гармонікою; (N \u003d 1) коливання з частотою - другий гармонікою (n \u003d 2), c частотою - n-й гармонікою.

Вираз (1) з використанням тотожності

може бути переписано у вигляді

, (2)

Коефіцієнти і визначається за формулами

Величина висловлює середнє значення функції за період, вона, називається також постійної складової і обчислюється за формулою

Формули (3) вирішують задачу аналізу : По заданій періодичної функції потрібно знайти коефіцієнти Фур'є і. Формули (1) і (2) вирішують задачу гармонійного синтезу : По заданим коефіцієнтам і потрібно знайти періодичну функцію.

Аналіз спектру послідовності прямокутних імпульсів

Сукупність амплітуд і частот гармонійних складових називають амплітудної-частотної характеристикою(АЧХ), а залежність від частот гармонік фазо-частотної характеристикою (ФЧХ).Амплітудно-частотний спектр прямокутних імпульсів може бути представлений графічно рис.2.

Рис.2. АЧХ і ФЧХ періодичної послідовності

прямокутних імпульсів.

Нехай, що представляє послідовність прямокутних імпульсів рис.1 з амплітудою, тривалістю і періодом описується рівнянням

Тоді амплітуди і фази для гармонійних складових визначаються рівнянням:

(4)

Величина називається скважностью і позначається буквою. Тоді рівняння (4) приймають вид

де n \u003d 1, 2, .... (5)

Для обчислення потужності сигналів представлених поруч Фур'є в теорії інформації використовують формули в яких значення опір R \u003d 1 Ом. У цьому випадку напруги u і струми i рівні, оскільки i \u003d u / R.

Потужність постійної складової Р 0 буде

а потужність змінної складової Р n для n-ї гармоніки

(6)

Формула для результуючої потужності набуде вигляду

ЗАВДАННЯ

1. Виконайте аналіз періодичної послідовності прямокутних імпульсів

1.1 За номером варіанту N, отриманого у викладача, визначте з таблиці 1 значення шпаруватості і кругової частоти .

Таблиця 1

№, вар	q	, Рад / с	№, вар	q	, Рад / с
	3,24	47,25		8,50	69,22
	6,52	97,50		6,72	78,59
	5,93	14,45		2,30	19,44
	7,44	15,12		3,59	37,96
	1,87	70,93		4,48	78,27
	5,46	91,65		2,99	42,48
	6,40	86,40		6,18	75,45
	1,27	48,98		1,81	57,64
	2,97	40,13		3,22	15,46
	1,09	85,95		3,66	55,25
	2,13	57,30		3,27	27,58
	7,99	66,90		4,64	3,68
	4,61	31,55		3,71	43,73
	1,95	25,24		4,33	70,44
	2,66	6,61		3,38	52,07
	1,10	18,37		6,92	26,17
	4,06	70,24		4,95	55,52
	2,40	35,10		6,51	82,64
	9,42	33,96		3,32	68,07
	6,13	43,25		7,75	32,49
	7,36	52,37		5,71	26,68
	2,33	24,84		2,42	96,02
	2,18	25,34		16,99	88,59
	5,80	12,99		62,23	50,21
	1,68	41,16		37,54	20,70

1.2 а) Визначте 11 перших значень коефіцієнтів un (n \u003d 0, 1, 2, ..., 10), вважаючи Е \u003d 1 В, використовуючи електронні таблиці "Exel" (або калькулятор, або інший програмний продукт) за формулами (5 ) і і внесіть їх до відповідного рядка un таблиці 2.

1.3 б) Розрахуйте потужності p n і запишіть їх у таблицю 2.

Таблиця 2

w		w 1	2w 1	…	10w 1
u n	u 0	u 1	u 2	…	u 10
j n	j 1	j 2	j 3	…	j 10
p n	p 0	p 1	p 2		p 10

і графіка амплітудно-частотної характеристики (АЧХ) рис.3, а).

1.4 Побудувати фазо-частотну характеристику (ФЧХ) періодичної послідовності імпульсів подібно рис.2) в якій зміна знака u n еквівалентно зсуву фази на p.

1.5 Розрахуйте питому (на опорі 1 Ом) потужність спектра перших 10 гармонік по формулі

.

2. Завдання синтезу.

2.1. Використовуючи рівняння (1), уявіть суму перших 10 гармонік підставивши у вигляді рівняння

за обчисленими в таблиці значень u n для,,, .... і побудуйте тимчасову залежність на періоді Т, наприклад.

з таблиці 3

у вигляді графіка 4 в тимчасовому діапазоні одного періоду Т \u003d, використовуючи поточний час t \u003d nD t -t / 2, з кроком де n \u003d 0,1,2, ..., 10, Показаного на рис. 3.

Мал. 3. Часовий інтервал для синтезу сигналу